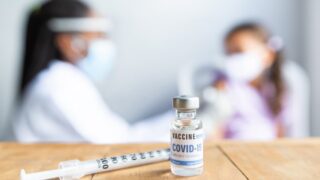
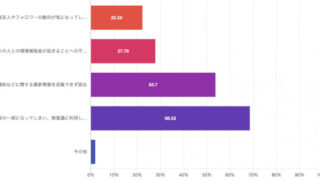
地球平面説を信じるジェラン・カンパネラ氏は、映画「ビハインド・ザ・カーブ -地球平面説-」の中で地球平面説を証明するための実験を行いましたが、逆に地球が球体であることを証明する結果が得られました。
Interesting | MCToon
https://mctoon.net/interesting/
カンパネラ氏の実験では、海抜0mの地点の片側にカメラを設置し、3マイル(約4.8km)離れた逆側では明るいライトを持ったアシスタントが立ちました。その間には穴の空いた2枚のボードが置かれ、カメラやライト、穴の高さはそれぞれ地面から17フィート(約5.1m)でした。
もしも地球が平面の場合、穴の空いた板を通してライトの光はカメラに映るはずです。しかしカンパネラ氏の実験ではライトの光が映ることはありませんでした。

次にカンパネラ氏は、1平方マイルあたり8インチ(約20cm)光は落下するという公式を使い、3マイルで6フィート(約1.8m)光が落下すると予測しました。そこでカメラや板の穴の位置は変えずに、ライトの高さを23フィート(約7m)まで上げ実験を行ったところ、ライトの光は映りませんでした。
科学系ブログのMCToonによると、カンパネラ氏の3マイルで6フィート光が落下するという予測は正しかったものの、その間にある板の穴の位置が低すぎたため、失敗してしまったとのこと。
実際に光の正しい高さを検証するためには、光の経路をたどり、カメラまでの3マイル全体での光の経路の最低の地点を計算する必要があるとのこと。

MCToonはPython上で動作するプログラムを作成し、計算を行っています。最低の地点はカメラと板との中間で、ライトから2.25マイル(約3.6km)の位置です。

さらに、先ほどの公式を用いると、光が落ちる最低の高さは40.5インチ(約1m)です。
最低の地点の後の0.75マイル(約1.2km)で光の経路はカメラの高さまで4.5インチ(約11.4cm)上昇することで、カメラに光が届くようになるとのこと。
しかし現実では天候によって変化する屈折の影響が及びます。屈折率が高いほど予測される光の高さは低くなるそうです。
夜間の地上の屈折率である+0.167とすると、屈折を含む光の落差は1平方マイルあたり6.67インチ(約17cm)となり、光が落ちる最低の高さは33.76インチ(約86cm)になります。最低の高さからのカメラまでの上昇幅は3.75インチ(約10cm)で、屈折を含むライトからカメラまでの距離は2.5フィート(約76cm)と計算されるとのこと。
よって17フィートの高さにあるカメラに光を映すためには地面から19.5フィート(約5.9m)の高さにライトを設置する必要があります。

地球平面説の下では、今回の実験で光は決してカメラに届かず、結果として地球球体説を証明することになりました。しかしカンパネラ氏は雑草の影響でカメラに光が届かなかったとして、より高い標高での再実験を行い、地球平面説を証明することを考えています。
この記事のタイトルとURLをコピーする